Data Mining & Machine Learning
using WEKA Explorer
The 1R Classifier
The 1R (Holte’s 1R) classifier is
a simple machine learning algorithm that works surprisingly well on standard
data sets. Robert Holte developed 1R
learning algorithm that competes very well with cutting edge algorithms. Robert Holte did not advocate the use of 1R
algorithm versus other mainstream algorithms rather used the simple one
classifier to demonstrate that many real word datasets did not embody very
complex relations, therefore, do not warrant complicated learning algorithms. In
order to, use the 1R classifier, one must prepare the data to deal with such
issues as, contentious valued data, missing values, and greedy decisions, these
topics are beyond the scope of this article.
Below are the general steps of 1R
algorithm:
For
each attribute a, form a rule as follows:
For
each value v from the domain of a,
Select the set of instances
where a has value v.
Let c be the most
frequent class in that set.
Add the following clause to
the rule for a:
if a has value v then the
class is c
Finally,
calculate the classification accuracy of this rule.
Note:
Use the rule with the highest classification accuracy. The algorithm assumes
that the attributes are
Discrete.
(Manning , Holmes & Ian,
1995).
Lets go over the required
software & setup.
Installation & Setup
1)
WEKA ,
required
2)
JDK &
JRE, required
3)
Any Java IDE
(Eclipse , Netbeans, etc...) , recommended
In order to download WEKA please
go to the following URL (http://www.cs.waikato.ac.nz/ml/weka/index.html)
Setting up your environment
1)
Please
download the latest JDK (Java Development Kit) & JRE (Java Runtime) , as
WEKA is written in Java.
JDK
(http://www.oracle.com/technetwork/java/javase/downloads/index.html)
2)
Make sure
that your PATH & CLASSPATH system variables point to JRE & JDK’s bin
directory.
Setting up your environment in Windows via GUI.
Go to Start , type “cmd” in the “Search programs and files” box Windows Command Prompt will appear
Go to Start , type “cmd” in the “Search programs and files” box Windows Command Prompt will appear
Checking Java
a) Check value of CLASSPATH by typing
this command “echo %CLASSPATH%”
You should see all paths that are
in CLASSPATH and should see your JDK’s bin folder
b) In order to check whether the JDK is setup
properly and whether JDK is available for compile your JAVA source globally ,
please type this command “javac”
You should see all “javac” command options printed out
Open WEKA
1)
Let’s check,
if WEKA has been installed & running. Go Start, WEKA folder, such as (Weka
3.6.9) open the folder, click on WEKA icon. You should see a small GUI application
open, click on Explorer button.
The Explorer
should open
1)
A brief
explanation of the the WEKA Explorer panels.
·
Preprocess
tab, is where the data can be loaded. The panel will let one view,edit, and
save the uploaded data.
·
Classify
tab, I where the classification algorithms can be accessed.
·
Visualize
tab, data can be viewed in graphical plots. Importing our example data set into
WEKA.
2)
The Iris
data set is probably one of the most cited data sets in data mining, machine
learning, and statistics studies, I obtained a copy from http://repository.seasr.org/Datasets/UCI/arff/iris.arff.
Data Set (Snippet
of the Iris Data set)
@RELATION iris
@ATTRIBUTE sepallength REAL
@ATTRIBUTE sepalwidth REAL
@ATTRIBUTE petallength REAL
@ATTRIBUTE petalwidth REAL
@ATTRIBUTE class {Iris-setosa,Iris-versicolor,Iris-virginica}
@DATA
5.1,3.5,1.4,0.2,Iris-setosa
4.9,3.0,1.4,0.2,Iris-setosa
4.7,3.2,1.3,0.2,Iris-setosa
4.6,3.1,1.5,0.2,Iris-setosa
Convert CSV data to “.arff” file (Optional
Section)
Now most data in the world isn’t
formatted for any format & the data miners or programmers have to prepare
the data before using any tool. The format WEKA uses is “arff” , which is not a
common format outside of the data mining world. Fortunately, WEKA provides Java
code that will convert CSV (comma separated values) to “arff” format file
If your data isn’t in “arff”
format follow this section & mini example, else skip it , and go Opening Opening The Data Set.
1)
Since the
data set is small , I’m going to paste it into Microsoft excel first.
(If the data
set were very large one would gave write a program to convert the data’s format
to CSV )
2)
I manually
pasted the data set below in Excel and , than go to File, Save As , Save as
type option list, select CSV (Comma delimited), click Save, & click ok for
all other warnings.
3)
Also do
“Find & Replace” all “|” to commas “,” than Save again.
As you start
you becoming a data miner, or data analyst, or any field that deals with data
you will realize that formatting the data , and ensuring data integrity is
probably as hard as data mining and will consume a great deal of any “real
world” project.
4)
Fortunately,
the WEKA people were wise enough to provide us with a way to convert CSV to
“arff” format files. However a user unfriendly way.
Go to your
Java IDE & create a simple Java project & paste the code below:
/*
Program
usage :
command line
argument 0 “args[0]” is the path of CSV file you want to convert
Example :
C:/Users/anaim/Desktop/Data Mining/OneR/Golf.csv
command line
argument 1 “args[1]” is the path & name that you will like to save the
.arff file
Example :
C:/Users/anaim/Desktop/Data Mining/OneR/Golf.arff
Remember
when passing paths in Java one most change backslashes “\” to forward “/” slashes.
*/
import weka.core.Instances;
import
weka.core.converters.ArffSaver;
import
weka.core.converters.CSVLoader;
import java.io.File;
public class CSV2Arff {
/**
* takes 2 arguments:
* - CSV input file
* - ARFF output file
*/
public static void main(String[] args) throws
Exception {
if (args.length != 2) {
System.out.println("\nUsage:
CSV2Arff <input.csv> <output.arff>\n");
System.exit(1);
}
// load CSV
CSVLoader loader = new CSVLoader();
loader.setSource(new File(args[0]));
Instances data = loader.getDataSet();
// save ARFF
ArffSaver saver = new ArffSaver();
saver.setInstances(data);
//I switched the order of the
setDestination() call with setFile() as the original code had a bug
saver.setDestination(new File(args[1]));
saver.setFile(new File(args[1]));
saver.writeBatch();
}}
Make sure to
add the “weka” jar to your projects build path , in order to be able to access
WEKA CSV to arff capabilities used in the Java code above, see below for
snapshot of this process:
Now if your
using Eclipse right click on your project , click run configurations, select
the “Arguments” tab, see the snapshot below:
Opening Opening The Data Set
Finally , Go to the WEKA Explorer
and select “Open file…” option & navigate to the path of your data set
(Example Golf.arff).
You should see a screen similar
to the one below , and also your attributes “sepallength, sepalwidth,humidity,
petallength, petalwidth, and class” listed on the left.
Interpret this information, well below is snippet of the “Classifier output” window:
=== Classifier model (full
training set) ===
petallength:
<
2.45 -> Iris-setosa
<
4.85 -> Iris-versicolor
>=
4.85 -> Iris-virginica
(143/150 instances correct)
=== Summary ===
1)
Correctly
Classified Instances 140 93.3333 %
2)
Incorrectly
Classified Instances 10 6.6667 %
3)
Kappa
statistic
0.9
4)
Mean
absolute error 0.0444
5)
Root mean
squared error 0.2108
6)
Relative
absolute error 10 %
7)
Root
relative squared error
44.7214 %
8)
Total Number
of Instances 150
=== Detailed Accuracy By Class
===
TP Rate FP Rate
Precision Recall F-Measure
ROC Area Class
1 0 1 1 1 1 Iris-setosa
0.88 0.04
0.917 0.88 0.898
0.92 Iris-versicolor
0.92 0.06
0.885 0.92 0.902
0.93 Iris-virginica
Weighted Avg. 0.933
0.033 0.934 0.933
0.933 0.95
=== Confusion Matrix ===
a b c
<-- classified as
50
0 0 | a = Iris-setosa
0 44 6 | b = Iris-versicolor
0 4 46 | c = Iris-virginica
Interpretation of OneR results
The “Classifier model (full
training set)” section shows the rules that were discovered, in order to
predict the classes (Iris-setosa, Iris-versicolor, Iris-virginica).
The rules that were discovered
are:
petallength:
<
2.45 -> Iris-setosa
<
4.85 -> Iris-versicolor
>=
4.85 -> Iris-virginica
We can interpret the above rules
using a simple algorithm:
IF petallength <2.45 , RETURN Iris-setosa
Else if petallength <4.85, RETURN
Iris-versicolor
ELSE RETURN Iris-virginica
In the “Summary” section the 1st
line states that 93.3% of the instances were correctly classified that is 140
out of 150 total instances, and the 2nd line states the number of
incorrectly classified instances which is 6.67% using the discovered rules.
Confusion Matrix -
There is nothing confusing about
a “confusion matrix” , which uses
tabular format to display performance results per class. Each class has its row
and column , were actual class is the number in the row and the predicted class
is the number in the column. For 2 Class prediction there is 2x2 matrix (not
counting row/column labels) , see below:
| |
Predicted Class
| ||
YES
|
NO
| ||
Actual Class
|
YES
|
True Positive (TP)
|
False Negative (FN)
|
NO
|
False Positive (FP)
|
True Negative (TN)
| |
True positives and true negatives
are correct classifications, false positives and false negatives are incorrect
classifications.
The final success rate of your
learning method is the number of correct classifications (TP + TN) divided by
total number of all classifications ( TP +TN /
TP+TN + FP+ FN) and the error rate is 1 – success rate.
In our example , we have 3
classes (Iris-setosa, Iris-versicolor, Iris-virginica) whoich will yield a 3x3
matrix (not counting row/column labels), see below:
=== Confusion Matrix ===
a b c
<-- classified as
50
0 0 | a = Iris-setosa
0 44 6 | b = Iris-versicolor
0 4 46 | c = Iris-virginica
I reformatted the original WEKA
text output to appear more visually understandable:
a
|
b
|
c
| |
a =
Iris-setosa
|
50
|
0
|
0
|
b =
Iris-versicolor
|
0
|
44
|
6
|
c =
Iris-virginica
|
0
|
4
|
46
|
Now we can measure the success rate of the 1R classifier on the Iris data set , success rate = all numbers in the diagonal (true classifications / entire sum) = 50+44+46 / 50+44+46+4+6 = 150/160 = 93.75% success rate , and 6.75% error rate.
Kappa Statistic –
The Kappa Statistic is the
percentage of possible predictions correctly classified by chance. The Kappa
statistic is derived by using a random classifier.
Mean
absolute error -
Is the average measure of how close
predictions are to actual values.
Reference
(http://en.wikipedia.org/wiki/Mean_absolute_error).
Root mean squared error -
Is the
measure of how well linear formula (y=
mx+b) or non-linear formula (polynomial
curve or exponential curve) fits the actual data if you were to put them side
by side on a regular graph. F(x) i the
calculated values from your formula & “y” is the actual value, and “n” is
the total number of data points.
Relative
absolute error -
Given
some value v and its approximation vapprox, the absolute
error is
Root
relative squared error -
the relative
error is
References
1)
Witten, I., Frank, E., & Hall, M. (2011). Data mining ,
practical machine learning tools and techniques. (3rd ed., Vol. 1, pp.
163-167). Burlington , MA: Morgan Kauffman.
2)
Manning , N., Holmes, G., & Ian, H. (1995). The development of
holte’s 1r classifier. Department of Computer Science,, Retrieved from
http://www.cs.waikato.ac.nz/ml/publications/1995/Nevill-Manning95-1R.pdf











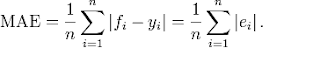


No comments:
Post a Comment